Arranjo e Combinação
Teoria
Para entendermos esses dois assuntos, devemos considerar um grupo de n elementos distintos e nos perguntarmos quantas maneiras existem de selecionar um subconjunto de tamanho p desse grupo. Por exemplo, no Campeonato Brasileiro de Futebol Masculino da Primeira Divisão, os 4 primeiros clubes dentre os 20 participantes estarão classificados à Taça Libertadores da América do ano seguinte, portanto, quantos agrupamentos distintos de 4 grupos poderemos formar com os 20 clubes? Isso é combinação, onde a ordem dos elementos não é relevante.
Podemos explicar o arranjo utilizando esse mesmo exemplo, mas seria um pouco diferente, já que no arranjo deveremos levar em conta a ordem dos elementos. O problema ficaria assim: No Campeonato Brasileiro, quantas possibilidades existem levando em conta o campeão, o vice-campeão, o terceiro e o quarto colocados? É importante ver que o conjunto 1 {Cruzeiro, São Paulo, Internacional, Corinthians} é diferente do conjunto 2 {Corinthians, Internacional, São Paulo, Cruzeiro}. Na combinação, essa ordem não importa, já que os 4 estarão classificados para a Taça Libertadores da América. No arranjo, essa ordem importa, uma vez que o Cruzeiro sendo campeão e o São Paulo vice no conjunto 1 é diferente do Corinthians campeão e do Internacional vice no conjunto 2.
Para o cálculo do 1° exemplo, usaremos a fórmula C = n!/[p!(n-p)!] - onde o símbolo de exclamação (!) significa fatorial (para mais informações sobre, consultar a página sobre fatorial neste blog). Substituindo n por 20 (quantidade de clubes participantes do campeonato) e p por 4 (quantidade de clubes classificados), teremos C = 20!/[4!(20-4)!]. Podemos simplificar
C = 20*19*18*17*16!/4!*16!, então C = 20*19*18*17/4*3*2*1. Resolvendo a fórumla, temos C = 4845.
No 2° exemplo, usaremos uma fórmula similar, onde A = n!/(n-p)!. Note que a única diferença daqui para a equação da combinação é que o termo (n-p)! no denominador não é multiplicado por p!. Substituindo os valores, obtemos
A = 20!/(20-4)!. Simplificando, A = 20*19*18*17*16!/16!, então A = 20*19*18*17, ou seja A = 116280.
Note que temos 4845 possibilidades diferentes de agrupamentos de clubes classificados à Taça Libertadores da América. Já para as 4 primeiras colocações, obteremos 116280 maneiras de arranjar os 4 primeiros colocados do campeonato na ordem. Verificamos que as possibilidades são enormes e todas podem acontecer, por isso o esporte é tão interessante.
Exercício - campeonato
Ainda utilizando o Campeonato Brasileiro de Futebol Masculino da Primeira Divisão como exemplo, queremos saber quantos jogos poderemos realizar no sistema de turno e returno, com os 20 times se enfrentando entre si.
Como estamos falando de turno e returno, cada time joga com cada time duas vezes, considerando os 20 times, tomamos o arranjo de 20 a 2 ou
A 20,2 = 20!/(20-2)!, resolvendo o 20 fatorial, A 20,2 = 20*19*18!/18!, simplificando,
A 20,2 = 20*19, resolvendo os termos, A 20,2 = 380 jogos.
Usamos o arranjo para este cálculo já que o jogo Chapecoense x Joinville difere do jogo Joinville x Chapecoense, senão, usaríamos a combinação (em um campeonato de apenas um turno).
Exercício - pratos
De um total de 6 pratos à base de carboídratos e 4 pratos à base de proteínas, pretendo fazer o meu prato com 5 desses itens. Os itens devem ser diferentes, e conter ao menos 2 proteínas. Qual é o número máximo de pratos distintos que poderei fazer?
Se não houvesse a restrição das duas proteínas, o cálculo seria simplesmente C10, 5:
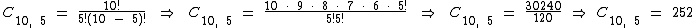
Se não houvesse a restrição das duas proteínas, o cálculo seria simplesmente C10, 5:
Poderíamos ter resolvido este exercício de uma outra maneira. Vamos lhe explicar como e vamos lhe dar o resultado, mas
o desenvolvimento em si você mesmo deverá fazer, para que consiga fixar melhor os conhecimentos adquiridos. Por favor, não deixe de fazê-lo.
O produto C6, 3 . C4, 2 = 20 . 6 = 120 nos dá o total de pratos contendo 3 itens de carboidrato e 2 itens de proteína.
Já o produto C6, 2 . C4, 3 = 15 . 4 = 60 é igual ao total de pratos contendo 2 itens de carboidrato e 3 itens de proteína.
Por fim o produto C6, 1 . C4, 4 = 6 . 1 = 6 resulta no total de pratos contendo 1 item de carboidrato e 4 itens de proteína.
Somando 120, 60 e 6, obtemos o mesmo resultado obtido anteriormente.
Portanto, o número máximo de pratos distintos que poderei fazer, contendo ao menos dois itens de proteína, é igual a 186 pratos.